Olá pessoal! Este é o lugar perfeito para Somar, Subtrair,Multiplicar e Dividir problemas e soluções matemáticas.Uma abraço virtual!
sábado, 22 de agosto de 2015
sábado, 18 de julho de 2015
Exercícios de Análise Combinatória
Questões e resoluções
Questão 1 - De quantas maneiras diferentes um técnico pode escalar seu time de basquete tendo á sua disposição 12 atletas que jogam em qualquer posição.
2!/ (12-5)! . 5!= 792
Questão 2 - No jogo de truco cada jogador recebe 3 cartas de um baralho de 40 cartas ( são excluídas as cartas 8,9 e 10) de quantas maneiras diferentes um jogador pode receber suas cartas ?
C(40,3) = 40!/ (40-3)! .3! = 40! / 37! / 3! = 40 x 39 x 38 / 3 x 2 = 9880.
Questão 3 - Quantas equipes de 3 astronautas podem ser formadas com 20 astronautas ?
C(20,3)! = 20!/(20-3)! .3! = 20x19x18)/(3x2x1) = 10x19x6 = 19x60 = 1140
Questão 4 - Quantas Diagonais tem um decágono ?
Para calcular a quantidade de diagonais em polígonos, devemos usar a fórmula
d = n(n-3) / 2
d = diagonal n = número de lados
resolvendo o decágono (10 lados) fica:
d = 10(10-3) / 2
d = 10 (7) / 2
d = 70 / 2
d = 35 diagonais
d = n(n-3) / 2
d = diagonal n = número de lados
resolvendo o decágono (10 lados) fica:
d = 10(10-3) / 2
d = 10 (7) / 2
d = 70 / 2
d = 35 diagonais
Questão 5 - Quantos números de 4 algarismos distintos maiores que 2000 podemos formar com os algarismos 1,2,3,4,5 e 6
ABCD => cada letra representa um espaço de algarismo.
no espaço A existem 5 algarismos válidos
no espaço B existem 5 algarismos pois são algarismos distintos...
no espaço C existem 4 algarismos disponiveis
no espaço D existem 3 algarismos disponiveis
logo : 5x5x4x3= 300 R: 300 números
no espaço B existem 5 algarismos pois são algarismos distintos...
no espaço C existem 4 algarismos disponiveis
no espaço D existem 3 algarismos disponiveis
logo : 5x5x4x3= 300 R: 300 números
Questão 6 - Em um grupo de 4 rapazes e 7 moças quantas comissões de 2 rapazes e 2 moças podemos formar ?
C7,2 x C4,2
C7,2 = 21
C4,2 = 6
Quantidade de maneiras diferentes =21x6
São então 126 maneiras diferentes
C7,2 = 21
C4,2 = 6
Quantidade de maneiras diferentes =21x6
São então 126 maneiras diferentes
Questão 7 - Uma sorveteria oferece 10 sabores, se uma pessoa tomar 3 bolas de sorvete do mesmo sabor ou não quantas as opções diferentes ela tem ?
10.10.10=1000
Questão 8 - Qual é o número de jogos em um campeonato com 20 clubes com turno e returno ?
(Dado: a Referência: turno e returno significa que cada time joga duas vezes entre si)
C(20,2)= 20!/(20-2)!.2!= 190 Com o returno da 380 jogos
Questão 9 - De quantas maneiras diferentes podemos colocar 8 livros em 3 gavetas de modo que fiquem 2 na primeira gaveta, 3 na segunda e 3 na terceira ?
C(8,2) X C(6,3) =28 x 20 = 560 maneiras
Questão 10 - Em um grupo de 20 pessoas há 6 mulheres, quantas comissões de 4 pessoas podem ser formadas de modo que nelas haja pelo menos 1 mulher ?
Total de comissões:
C20,4=26!/4!16!=20x19x18x17/4x3x2 =4845
Comissões só com homens:
C14,4=14!/4!10!=14x13x12x11/4x3x2=1001
Comissões com pelo menos uma mulher:
4845 - 1001 =3844 comissões
C20,4=26!/4!16!=20x19x18x17/4x3x2 =4845
Comissões só com homens:
C14,4=14!/4!10!=14x13x12x11/4x3x2=1001
Comissões com pelo menos uma mulher:
4845 - 1001 =3844 comissões
terça-feira, 5 de maio de 2015
domingo, 26 de abril de 2015
10 sites para estudar Matemática de graça
Além de blogs matemáticos incluindo este , agora você também pode acessar um desses 10 sites para descobrir melhor os caminhos da matemática e começar a estudar. Vamos nessa pesquise, clique no link!
quinta-feira, 23 de abril de 2015
FUNÇÕES TRIGONOMÉTRICAS
Vamos estudar as funções trigonométricas seguintes:
y = sen x y = cos x y = tg x
e também os inversos destas funções, ou seja:
y = 1/sen x = cosec x y =1/ cos x = sec x y = 1/tg x = cotg x
O ângulo x é a variável independente e o valor da função é a variável dependente. É importante recordar que a medida dos ângulos pode expressar-se em graus ou em radianos. Assim, vemos que:
0°
0 rad
360°
2
rad
Observemos agora as principais características das funções já mencionadas:
Função Seno y = sen x
a) A função seno é periódica, já que: sen (x + 2
) = sen x
em que o período da função é t = 2
;
b) O domínio da função é todo o conjunto R, e o contradomínio da função é [-1,1];
c) O valor máximo da função é 1 em x =
/2 e o valor mínimo da função é -1 em x = 3
/2;
d) A função é contínua em todo o seu domínio;
e) É uma função crescente no intervalo [0,
/2] e [3
/2,2
], e decrescente no intervalo [
/2,3
/2];
f) A função é ímpar, já que: sen (-x) = - sen x e o gráfico é simétrico em relação à origem (0,0).
Função cosseno y = cos x
a) A função cosseno é periódica, pois: cos (x + 2
) = cos x
e o período da função é T = 2
;
b) O domínio é todo o conjunto dos números reais R, e o contradomínio da função é [-1,1];
c) O valor máximo da função é 1 em x = 0 ou x = 2
e o valor mínimo da função é -1 em x =
;
d) A função é contínua em todo o seu domínio;
e) É uma função crescente no intervalo [
,2
] e decrescente no intervalo [0,
];
f) A função é par, já que: cos x = cos (-x) e o gráfico é simétrico em relação ao eixo das ordenadas.
Função Tangente y = tg x
a) A função tangente é periódica, já que:
em que o período da função é t =
;
b) O domínio da função é R/ {
/2 - k
, k
Z }, e o contradomínio da função é todo o
conjunto R;
c) Esta função não tem extremos locais;
d) A função é contínua em todo o seu domínio;
e) É uma função crescente em todos os pontos do domínio;
f) A função é ímpar, pois: tg (-x) = - tg x e o gráfico é simétrico em relação à origem (0,0).
y = sen x y = cos x y = tg x
e também os inversos destas funções, ou seja:
y = 1/sen x = cosec x y =1/ cos x = sec x y = 1/tg x = cotg x
O ângulo x é a variável independente e o valor da função é a variável dependente. É importante recordar que a medida dos ângulos pode expressar-se em graus ou em radianos. Assim, vemos que:
0°
Observemos agora as principais características das funções já mencionadas:
Função Seno y = sen x
a) A função seno é periódica, já que: sen (x + 2
b) O domínio da função é todo o conjunto R, e o contradomínio da função é [-1,1];
c) O valor máximo da função é 1 em x =
d) A função é contínua em todo o seu domínio;
e) É uma função crescente no intervalo [0,
f) A função é ímpar, já que: sen (-x) = - sen x e o gráfico é simétrico em relação à origem (0,0).
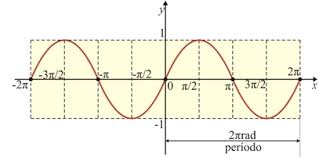
O gráfico
da função seno, no plano cartesiano, será uma curva denominada senóide. Atribuindo valores ao arco x,
pode-se chegar ao gráfico.
Função cosseno y = cos x
a) A função cosseno é periódica, pois: cos (x + 2
b) O domínio é todo o conjunto dos números reais R, e o contradomínio da função é [-1,1];
c) O valor máximo da função é 1 em x = 0 ou x = 2
d) A função é contínua em todo o seu domínio;
e) É uma função crescente no intervalo [
f) A função é par, já que: cos x = cos (-x) e o gráfico é simétrico em relação ao eixo das ordenadas.
O gráfico
da função cosseno, no cartesiano, será uma curva denominada co- senóide.
Atribuindo valores ao arco x, pode-se chegar ao gráfico.
Função Tangente y = tg x
a) A função tangente é periódica, já que:
tg
(x +
) = tg x
em que o período da função é t =
b) O domínio da função é R/ {
c) Esta função não tem extremos locais;
d) A função é contínua em todo o seu domínio;
e) É uma função crescente em todos os pontos do domínio;
f) A função é ímpar, pois: tg (-x) = - tg x e o gráfico é simétrico em relação à origem (0,0).
O gráfico
da função tangente, no cartesiano, será uma curva denominada tangentóite.
Atribuindo valores ao arco x, pode-se chegar ao gráfico.
domingo, 25 de janeiro de 2015
Quiz Matemático.
1º)Um homem entra numa livraria e compra, A viagem
pela Matemática, que custa 20 reais e paga com um anota de 100 reais. Sem
troco, o livreiro vai até a banca de jornal e troca a nota de 100 reais por 10
notas de 10 reais. O comprador leva o livro e 8 notas de 10 reais.Em seguida
entra o jornaleiro dizendo que a nota de 100 reais era falsa. O livreiro troca
a nota falsa por uma nota de 100 verdadeira. Sem dinheiro do troco, sem o livro
e a nota que deu ao jornaleiro, qual foi afinal o prejuízo do livreiro?
a)100 reais
b)180 reais
c)80 reais
d)20 reais
e)120 reais
2º) Uma data ...
Se o amanhã de ontem era quinta-feira, que dia é o dia depois de amanhã de ontem ?
a)Segunda - feira.
b) Terça – feira.
c)Quarta – feira.
d)Quinta – feira.
e)Sexta – feira.
Se o amanhã de ontem era quinta-feira, que dia é o dia depois de amanhã de ontem ?
a)Segunda - feira.
b) Terça – feira.
c)Quarta – feira.
d)Quinta – feira.
e)Sexta – feira.
a) No século XX
b)No século XIX
c)Em 1977
d)Em 1877
e)Em 1777
-Foi Ricardo, disse João.
-Fui eu, disse Eduardo.
-Foi Eduardo, disse Ricardo.
Somente um dos três dizia a verdade , e a mãe sabia que Eduardo estava mentindo. Então:
a)Ricardo além de mentir quebrou a vidraça.
b)João mentiu mas não quebrou a vidraça.
c)Ricardo disse a verdade.
d)Não foi Ricardo que quebrou a vidraça.
e)Quem quebrou a vidraça foi Eduardo ou João.-Fui eu, disse Eduardo.
-Foi Eduardo, disse Ricardo.
Somente um dos três dizia a verdade , e a mãe sabia que Eduardo estava mentindo. Então:
a)Ricardo além de mentir quebrou a vidraça.
b)João mentiu mas não quebrou a vidraça.
c)Ricardo disse a verdade.
d)Não foi Ricardo que quebrou a vidraça.
• Se Ari pede a mesma bebida que Carlos, então Bruna pede água.
• Se Ari pede uma bebida diferente da de Bruna, então Carlos pede suco.
• Se Bruna pede uma bebida diferente da de Carlos, então Ari pede água.
• Apenas um deles sempre pede a mesma bebida.
Quem pede sempre a mesma bebida e que bebida é essa?
(A) Ari; água
(B) Bruna; água
(C) Carlos; suco
(D) Ari; suco
(E) Bruna; suco
6º) Tijolos no caminhão - Um pequeno caminhão pode
carregar 50 sacos de areia ou 400 tijolos. Se foram colocados no caminhão 32
sacos de areia, quantos tijolos ele pode ainda carregar?
a)164
b)256
c)136
d)144
e)186
a)164
b)256
c)136
d)144
e)186
7º) Travessia no rio - Seu José e seus dois filhos Zezinho e Luizinho pretendem atravessar um rio. Só que eles não sabem como, pois o barco que possuem transporta com segurança até 100 quilogramas. Seu José pesa 100 quilogramas e cada um dos seus filhos pesa 50 quilogramas. E agora? Como eles poderão atravessar o rio com segurança?
8º)
Concurso inteligente - Você participa de um programa de televisão cujo
apresentador escondeu um prêmio no interior de uma das três caixas. Sabendo-se
que só uma caixa das três indicações é correta, em qual caixa se encontra o
prêmio? Caixa 1, caixa 2 ou caixa 3?
quinta-feira, 22 de janeiro de 2015
As TIC'S no Ensino da Matemática
As tecnologias de informação e
comunicação (TIC), mais o conjunto de
ferramentas que vem disponibilizando, podem enriquecer o ensino da Matemática,
valorizando uma abordagem experimental de conceitos em domínios tão importantes
como a geometria e a modelagem de
fenômenos reais.
Assinar:
Comentários (Atom)