FUNÇÕES TRIGONOMÉTRICAS

Vamos estudar as funções trigonométricas seguintes:

y = sen x                              y = cos x                                 y = tg x

e também os inversos destas funções, ou seja:

y = 1/sen x = cosec x               y =1/ cos x = sec x                         y = 1/tg x = cotg x

O ângulo x é a variável independente e o valor da função é a variável dependente. É importante recordar que a medida dos ângulos pode expressar-se em graus ou em radianos. Assim, vemos que:

0° 0 rad                                                                          360° 2 rad

Observemos agora as principais características das funções já mencionadas:

Função  Seno    y = sen x

a) A função seno é periódica, já que:  sen (x + 2 ) = sen x   em que o período da função é t = 2 ;

b) O domínio da função é todo o conjunto R, e o contradomínio da função é [-1,1];

c) O valor máximo da função é 1 em x = /2 e o valor mínimo da função é -1 em x = 3 /2;

d) A função é contínua em todo o seu domínio;

e) É uma função crescente no intervalo [0, /2] e [3 /2,2 ], e decrescente no intervalo [ /2,3 /2];

f) A função é ímpar, já que: sen (-x) = - sen x      e o gráfico é simétrico em relação à origem (0,0).

O gráfico da função seno, no plano cartesiano, será uma curva denominada senóide. Atribuindo valores ao arco x, pode-se chegar ao gráfico.

Função cosseno   y = cos x

a) A função cosseno é periódica, pois:    cos (x + 2 ) = cos x       e o período da função é T = 2 ;

b) O domínio é todo o conjunto dos números reais R, e o contradomínio da função é [-1,1];

c) O valor máximo da função é 1 em x = 0 ou x = 2 e o valor mínimo da função é -1 em x = ;

d) A função é contínua em todo o seu domínio;

e) É uma função crescente no intervalo [ ,2 ] e decrescente no intervalo [0, ];

f) A função é par, já que:     cos x = cos (-x)     e o gráfico é simétrico em relação ao eixo das ordenadas.

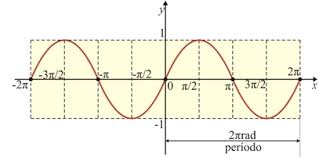
O gráfico da função cosseno, no cartesiano, será uma curva denominada co- senóide. Atribuindo valores ao arco x, pode-se chegar ao gráfico.

Função  Tangente       y = tg x 

a) A função tangente é periódica, já que:

tg (x + ) = tg x

em que o período da função é t = ;

b) O domínio da função é R/ { /2 - k , k Z }, e o contradomínio da função é todo o conjunto R;

c) Esta função não tem extremos locais;

d) A função é contínua em todo o seu domínio;

e) É uma função crescente em todos os pontos do domínio;

f) A função é ímpar, pois:   tg (-x) = - tg x         e o gráfico é simétrico em relação à origem (0,0).

O gráfico da função tangente, no cartesiano, será uma curva denominada tangentóite. Atribuindo valores ao arco x, pode-se chegar ao gráfico.